
Program EBOP byl vytvořen Etzelem (1981) na základě sférického modelu NDE (Nelson & Davis 1972). NDE model a jeho předpoklady jsou blízké rektifikačnímu modelu Russella a Merrilla (1952), ale protože počítá světelné křivky přímo, je pružnější a poskytuje možnost pozdějšího doplnění o další fyzikální jevy. Nicméně EBOP se záměrně opírá při řešení spíše o parametry definované na základě světelné křivky (Etzel 1993). Je vhodný pro řešení oddělených soustav s minimální deformací složek (teprve později byl program rozšířen i na možnost lehce deformovaných složek modelovaných jako elipsoidy.) - počítá tedy se sférickými složkami obíhajícími po kruhové nebo i výstředné trajektorii a s lineárním průběhem okrajového ztemnění dle vztahu
kde ϑ značí úhel mezi normálou k povrchu a libovolným směrem a index λ závislost na vlnové délce. Zakrývaná plocha hvězdy S a ztráta světla během zákrytu je integrována poloanalyticky použitím základních vztahů pro kruhové disky, prstence a výseče. Disk zakrývané hvězdy je rozdělen do soustředných prstenců o poloměru rsin ρ a šířce Δ ϑ = rcos ρ dρ, kde ρ je úhlová vzdálenost ke středu disku. Při integraci přes celý disk, je střední tok

Samozřejmě přesnost výpočtu závisí na šířce Δϑ prstenců a přesnosti prováděných dílčích výpočtů. Ukazuje se, že Δϑ =5° vede k dostatečně přesným výsledkům (s relativní chybou 10-4). Výhodou použitého poloanalytického řešení je zejména jeho výkonnost a efektivita. Je rychlejší a přesnější než standardní procedury založené na eliptických integrálech nebo čistě numerických postupech. EBOP určuje zejména tyto parametry:
a také přidružené parametry:
EBOP používá podobně jako Russellova-Merrillova metoda centrální povrchovou jasnost J2. Rozdíl spočívá v tom, že J2 je relativní vzhledem k povrchové jasnosti v centru disku primární hvězdy, která je definitoricky rovna jedné. Ve sférickém modelu hvězd NDE je totiž J2 přímo spojeno s poměrem hloubek minim, zatímco teploty mají jen nepřímý vliv na světelnou křivku. Výhodou parametru J2 oproti efektivním teplotám nebo poměru bolometrických svítivostí je to, že může být určen empiricky ze světelné křivky, zatímco teploty hvězd jsou spojeny se světelnou křivkou jen zprostředkovaně s užitím mnoha předpokladů modelu vyzařování. Pro lineární okrajové ztemnění lze tok záření z jednotkového disku o jednotkové centrální intenzitě zapsat ve tvaru
Nenormované svítivosti složek pak jsou
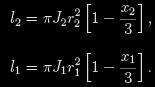
Poměr svítivostí
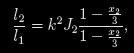
pak závisí jen na poměru poloměrů, poměru povrchových jasností a korekčním členu pro okrajové ztemnění. V normovaných jednotkách jsou pak relativní svítivosti samozřejmě
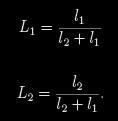
Je-li v soustavě detekováno třetí světlo, použije EBOP modifikovanou definici pro relativní svítivosti
EBOP nepodporuje přímé modelování deformace složek v důsledku nevelké vzdálenosti složek ani efektu odrazu. Nicméně umožňuje přidání opravných členů (Etzel 1981, str. 114-115), které jsou odvozeny zejména na základě práce Binnendijka (1960). Při řešení efektu odrazu vychází přitom z předpokladu, že osvětlující hvězda je bodový zdroj, která osvětluje přivrácenou hemisféru druhé hvězdy. Kvantitativní popis uvádějí už Russell a Merrill (1952; str. 44) nebo Binnendijk (1960;str. 119)
kde cos φ je směrový kosinus směru záření vzhledem ke spojnici středů obou složek a Θ je pravá anomálie. Svítivost primární složky se kvůli efektu odrazu mění podle
kde R1 je příspěvek nasvětlené hemisféry primární složky a A1 je bolometrické albedo, kterým se efekt odrazu zpravidla modeluje. Podobné vztah lze samozřejmě zapsat i pro sekundární složku. Celkovou změnu svítivosti soustavy dostaneme zahrnutím příspěvků obou složek. Jejich velikost závisí na fázi. Příspěvek od hvězdy v popředí je velmi malý, roste jen když se zakrývaná oblast S výrazně zmenšuje. Pozorovatel zaznamenává změny svítivosti
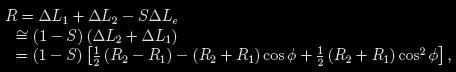
kde Δ Le je světlo odražené ze zakrývané hvězdy. Je zřejmé, že efekt odrazu způsobuje změny jasnosti mimo zákryty. Aby bylo možné určovat jasnosti v kvadratuře (Θ = 90°), byl pro řešení metodou nejmenších čtverců dodán volný normalizační parametr mq. Jestliže v soustavě žádný podstatný efekt odrazu není, pak mq je stejné jako hvězdná velikost v kvadratuře. EBOP je dostatečně přesný pro relativně jednoduché oddělené systémy se středním zploštěním menším než 0.04. Program byl oblíbený především v 70. a 80. letech minulého století pro vysokou přesnost integrace a podstatně kratší výpočetní čas ve srovnání s tehdy rozšířeným sofistikovanějším programem WINK (Wood 1972).
Inovovanou verzi programu JKTEBOP je možné nalézt na webu Johna Southworthahttp://www.astro.keele.ac.uk/~jkt/codes/jktebop.html
Literatura:
Binnendijk, L., 1960, Properties of double stars; a survey of parallaxes and orbits, Univ. of Pennsylvannia Press, Philadelphia
Etzel, P. B., 1981, A Simple Synthesis Method for Solving the Elements of Well-Detached Eclipsing Systems, v E. B. Carling a Z. Kopal (editoři), Photometric & Spectroscopic Binary Systems, NATO 1981, D. Reidel, Dordrecht, Holland
Etzel, P. B., 1993, Current Status of the EBOP Code, v Light Curve Modeling of Eclipsing Binary Stars, Springer, New York, ed. E. F. Milone, str. 113-124
Nelson, B., Davis, W. D., 1972, ApJ 174, 617
Russell, H., N., Merrill, J., E., 1952, Contrib. Princeton Univ. Observatory
Southworth J., Maxted P. F. L., Smalley B., 2004, MNRAS, 349, 547