Russell popsal princip své metody ve dvou statích (Russell 1912a,b). Kompletní popis světelné křivky je dle něj možný užitím nejméně 13 parametrů (a, e, w, i, P, t0, r1, r2, L1 , L2,+ alespoň tří dalších popisujících elongaci, okrajové ztemnění a efekt odrazu). Nicméně jeho model je zjednodušený a zpočátku uvažuje pouze sférické hvězdy bez okrajového ztemnění, které se pohybují se po kruhové dráze. Chtěl ze světelné křivky zjistit "jen" relativní rozměry a svítivosti složek a inklinační úhel. Další podmínkou je nenulový parametr d , tedy přítomnost fáze konstantní jasnosti v minimu. Navíc bylo nutné na počátku křivku rektifikovat, tedy odstranit možné efekty asféričnosti složek a efekt odrazu. To však samo o sobě snižovalo výslednou přesnost získaných parametrů.
I když se nejvíce setkáváme se světelnou křivkou jako závislostí hvězdné velikosti (vyjádřené v magnitudách) na čase, pro výpočet parametrů soustavy je vhodné světelnou křivku vyjádřit prostřednictvím svítivostí složek soustavy a ztráty svítivosti soustavy během zákrytu. Svítivost soustavy mimo zákryt daná součtem svítivostí složek nechť je rovna jedné L1+L2=1. Pak ztráta svítivosti soustavy při zákrytu je
(1)
kde L je svítivost soustavy v libovolné fázi zatmění. Ztrátu svítivosti soustavy během zatmění je možné vyjádřit pomocí tzv. fotometrické fáze
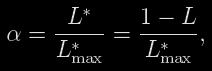(2)
kde L*max je ztráta svítivosti soustavy v okamžiku vnitřního dotyku disků hvězd. V případě úplného zatmění (menší složka je zakrývána větší) je pak
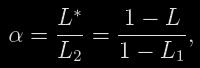(3)
Z geometrie situace (viz obrázek 1) vyplývá, že fotometrickou fázi lze vyjádřit také jako
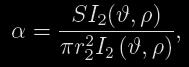(4)
kde S je zakrytá plocha a I 2 intenzita vyzařování jednotky disku vzdálené od středu ρ ve směru ϑ (viz obrázek 2).
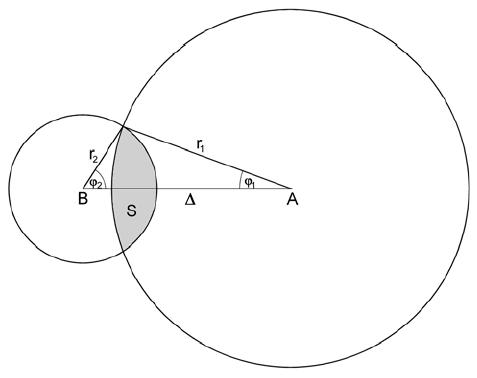
Schematický náčrt zatmění
Obecně lze intenzitu vyzařování vyjádřit vztahem
(5)
kde x je koeficient okrajového ztemnění a I 0 intenzita vyzařování ve středu disku. Pro stejnorodé disky1) (x= 0) platí I=I 0 a naopak pro maximální hodnotu okrajového ztemnění2) x = 1 se vztah (5) zjednoduší na I (ρ)=I 0 cos ϑ. Pro libovolnou hodnotu okrajového ztemnění 0<x<1<>(tzv. hypotézu X) lze fotometrickou fázi vyjádřit dle Ceseviče (ve Zverev a kol,.1947) vztahem
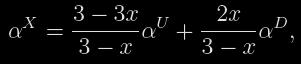(6)
kde αU a αD jsou fotometrické fáze při hypotéze U, resp. D pro dané hodnoty parametrů k a p, které jsou definovány jako poměr poloměrů k = r1/r2, resp. pomocí vzdálenosti středů disků hvězd Δ
(7)
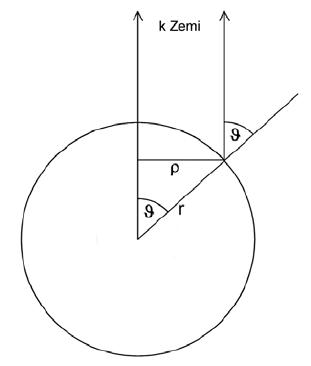
Zavedení veličin - vzdálenosti od středu disku hvězdy ρ a směrového úhlu mezi zorným paprskem a normálou k povrchu hvězdy ϑ .
Ukažme si postup řešení v případě nulových koeficientů okrajového ztemnění a úplného zatmění, tedy pro případ, kdy větší složka zcela zakrývá složku menší. Fotometrická fáze je pak definována vztahem
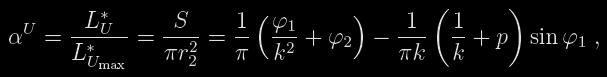(8)
kde φ1 a φ2 jsou úhly zobrazené na obrázku 1 a lze je vyjádřit jako
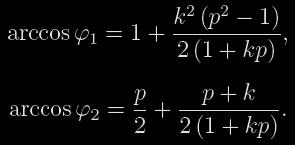(9,10)
Z výše uvedených vztahů je zřejmé, že fotometrická fáze závisí na parametrech p a k. Lze tedy psát αU =αU (k,p) . Russell však pro řešení potřeboval tuto funkci transformovat na p=p(α ,k). Vycházel přitom z rozboru geometrie úlohy. Řešením sférického trojúhelníku došel ke vztahu
(11)
kde
je fáze zatmění v čase Δ t prošlém od středu
minima. Nyní už p ve vztahu (11) opravdu vystupuje jako funkce k a α: p=p(α,k). Jsou
zde známy jen hodnoty Θ a α . Naopak neznámými jsou i, r1, k. Russell zavedl označení
φ (k,α)=1+kp(k,α) a vztah (11) přepsal do podoby
(12)
Nyní si Russell zvolil dvě hodnoty fotometrické fáze α2=0.6 a α3=0.9 a pro ně ze světelné křivky odečetl příslušné hodnoty Θ2 a Θ3. Těmto dvojicím hodnot odpovídají rovnice
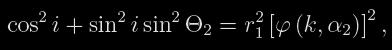(13)
(14)
Odečtením a podělením vztahů (12)-(14) zavedl Russell novou funkci
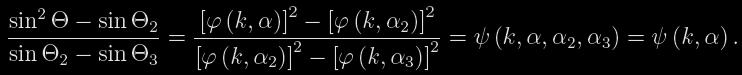(15)
Označíme-li A=sin2 Θ2 a B=sin2 Θ2 -sin2 Θ3, pak lze vztah (15) přepsat do podoby
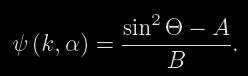(16)
Pro libovolné hodnoty α pak Russell odečetl ze světelné křivky odpovídající Θ a z tabulek funkce ψ(k,α) získal hodnotu k.
Popsaný postup měl ale jistá úskalí. Především - přesné určení hodnoty k z jednoho páru Θ a α je v podstatě nemožné. Do určení jsou vnášeny chyby zejména při odečítání hodnot ze světelné křivky a tyto chyby se poté přenášejí i do určení hodnot A a B. K dosažení nejlepší shody syntetické světelné křivky vypočtené z určených parametrů a napozorované světelné křivky je nutné mírně měnit získané hodnoty A a B. Stanovení hodnoty k pro různé hodnoty fotometrické fáze má různou váhu, určení je třeba opakovat a následně brát v úvahu výslednou průměrnou hodnotu.
Přes své nedostatky byla Russellova metoda velkým milníkem, proto jí také byla věnována větší pozornost, než by si snad ve srovnání s dnešními metodami zasloužila. Velmi záhy se dočkala řady vylepšení a modifikací - například Fetlaar (1923), Šarbe(1924), Hetzer(1931), Krat(1934, 1935, 1936), Piotrowski(1937), Schneller(1949), Kopal(1941). Nejvýznamnější a dlouho nejpoužívanější však byla modifikace Russella a Merrilla (1952).
Literatura:
Fetlaar, J., 1923, Rech. Ast. Obs. Utrecht IX, str. 1
Hetzer, E., 1931, dizertační práce, Leipzig
Kopal, Z., 1941, ApJ 94, 145
Krat, V. A., 1934, Astr. žurn. 11, 407
Krat, V. A., 1935, Astr. žurn. 12, 21
Krat, V. A., 1936, Astr. žurn. 13, 521
Piotrowski, S., 1937, AA(a) 4, 1
Russell, H., N., Merrill, J., E., 1952, Contrib. Princeton Univ. Observatory
Schneller, H., 1949, Veröffentlichungen der Sternwarte zu Sonneberg, Bd. 1, 4
Šarbe, S. B., 1924, Izv. GAO 10, No. 1
Poznámky:
1) V literatuře se tento případ označuje jako hypotéza U (z angl. uniform disk).
2) tzv. hypotéza D (z angl. darkened)
zpět na přehled metod