
Metoda je výrazným vylepšením původní Russellovy metody. V základní variantě je jednodušší, ale dává přesnější výsledky. Vychází ze stejných předpokladů jako původní metoda - například sférického tvaru složek, teprve později byl umožněn i tvar tříosého elipsoidu. Na světelné křivce se pak vyberou body pro fotometrické fáze αi= 0.05, 0.10, 0.20, 0.30, 0.50, 0.60, 0.70, 0.95, 0.97, 0.985 a najdou se pro ně odpovídající hodnoty Θi. Poté jsou body rozděleny do třech skupin (4 body, 3 body, 3 body) a pro ně spočítány hodnoty
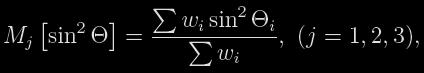 (1)
(1)
kde wi jsou určené váhy po řadě 2, 2, 2, 1, 1, 1, 1, 1, 2, 2. Nahradíme-li sin2 Θ veličinou M [sin2 Θ] a funkci ψ(k,α) obdobně funkcí Ψ 1), , je možné nyní přepsat (1) do soustavy rovnic ve tvaru
Odtud získáme
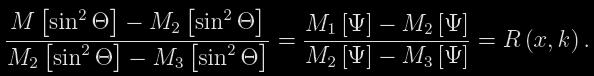 (3)
(3)
Tabulky hodnot funkcí Mj (Ψ) a R(x,k) spočítal Merrill pro případy přechodu menší složky před větší i zákrytu menší složky větším souputníkem. Z tabulek dostaneme nejdříve hodnotu k a následně i hodnoty konstant A a B. Další postup už je shodný s původní Russellovou metodou.
Velkou předností této metody oproti původní Russellově je určení konečných hodnot konstant A a B bez nutnosti jejich drobných variací pro dosažení shody syntetické světelné křivky s napozorovanou. Zavedením více bodů a jejich středováním s užitím vah se navíc zvýšila přesnost určení parametrů dvojhvězdy. Z hlediska astrofyzikálního je metoda omezena užitím Planckova vyzařovacího zákona, lineárního okrajového ztemnění a jednoduchého efektu odrazu, přesto byla významným příspěvkem při studiu těsných dvojhvězd. V sedmdesátých letech minulého století byla konečně převedena do počítačové podoby - Jurkevich 1970), Proctor & Linnell 1972. Stala se i inspirací pro tvůrce dalších programů na určování parametrů zákrytových dvojhvězd. Vycházely z ní prvotní verze nové generace programů EBOP a WINK.
1) Funkce Ψ závisí i na koeficientu okrajového ztemnění. Původní Russelova funkce ψ závisela jen na fotometrické fázi α a parametru k a byla spočítána pro hypotézy U a D. Teprve později Cesevič a Merrill spočítali tabulky hodnot funkce ψ i pro hypotézu X.
Literatura:
Russell, H. N.; Merrill, J. E.,Contributions from the Princeton University Observatory, Princeton: Observatory, 1952
Jurkevich, I., 1970, Vistas in Astronomy 12, 63
Proctor, D. D., Linnell, A. P., 1972, ApJ Supplement, 24, 449
zpět na přehled metod