Kopalova metoda (Frequency Domain Method)

Popis:
V roce 1975 publikoval Kopal první příspěvek (Kopal 1975), v němž představil nový přístup v analýze světelných křivek zákrytových dvojhvězd - metodu frekvenční analýzy. Tato práce byla první ze série 26 článků Kopala a jeho žáků a představuje použití nové metody na nejjednodušším případě dvou sférických hvězd obíhajících po kruhové trajektorii. Obecnější základy metody jsou popsány například v Kopal (1979) a také Kopal (1990, str. 41-69).
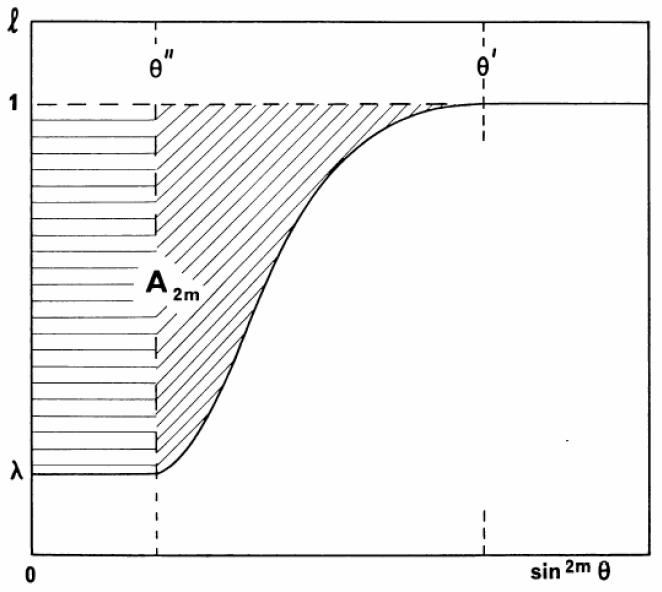
Na rozdíl od klasické analýzy světelné křivky, kde se věnuje pozornost jednotlivým bodům (fázový úhel θ; ztráta světla l) na světelné křivce, se Kopal zaměřil na plochu protilehlou ke světelné křivce vyjádřené v souřadnicích (l; sin2mθ), kde m=1, 2, 3, ... (viz obrázek). Plocha A2m omezená přímkami l=1, sin2mθ =0 a aktuální křivkou je zřejmě dána
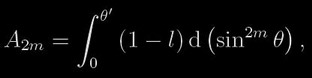 (1))
(1))
kde θ' odpovídá fázovému úhlu prvního kontaktu. Ukažme si Kopalův přístup k řešení na nejjednodušším případě úplného zatmění. Moment zatmění A2m lze zapsat také jako
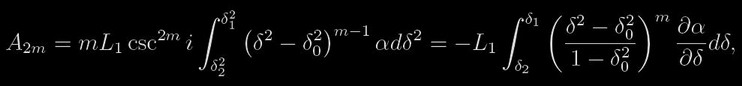 (2)
(2)
kde α je fotometrická fáze, δ znamená vzdálenost složek tak, že δ0 = cos i je vzdálenost v největším přiblížení (pro θ = 0) a δ1 a δ2 jsou vzdálenosti při prvním a druhém kontaktu a L1 = 1 - λ, kde λ je pozorovaná ztráta svítivosti během zatmění. Vztah (3) lze vyjádřit pomocí parciálních integrálů typu
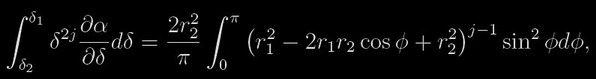 (3)
(3)
pro j= 0, 1, 2, ... Pro j>0 je pravá strana jednoduše řešitelná, pro j=0 platí zřejmě
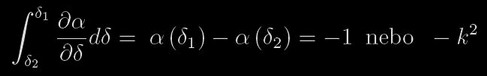 (4)
(4)
podle toho, zda jde o zákryt r1<r2 nebo transit r1>r2. Pak pro hodnoty m = 1, 2, 3, ... lze najít vztahy
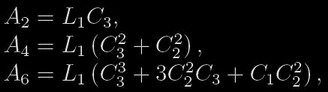 (5)
(5)
kde koeficienty Ci mají následující význam
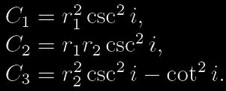 (6)
(6)
Jestliže určíme z pozorované světelné křivky například integrací plochy A2,A4,A6, dosadíme je do rovnic (5), vypočteme hodnoty koeficientů C1, C2, C3 a přepíšeme (6) do podoby
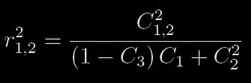 (7)
a
(7)
a
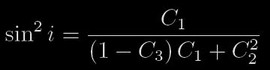 (8)
(8)
dostaneme požadované parametry dvojhvězdy. Jak již bylo poznamenáno, výše uvedený postup řešení je demonstrován na nejjednodušším možném případu, postupně ale byla metoda dále rozvíjena a přibyly různé korekce, postihují okrajové a gravitační ztemnění, slapově deformované nesférické složky a podobně (Kopal 1989,1990). Pro křivky s odchylkami od nejjednoduššího modelu je přitom postup řešení následující:
- určit nezbytný počet momentů světelných křivek (aspoň 4);
- vypočítat nezbytný počet konstant Cj=1,n (aspoň 4) z maxima světelné křivky a vzít jejich váhovaný
- vypočítat (normované) momenty;
- vypočítat hodnoty r1, r2, i, L1, L2 z momentů;
- vypočítat světelné křivky z elementů a určit perturbace P2m;
- použít perturbační členy k získání zlepšených momentů;
- opakovat kroky 3-6 a iteracemi získat konečný soubor elementů.
Kopal tvrdil, že žádné běžné časové analýzy1) nemohou využít empirická data, aby převedly pozorovanou světelnou křivku do podoby, odkud by bylo možné přímo určit elementy. Řada autorů to však odmítá. Kopalem prohlašovaná vyšší úroveň jeho metody nebyla dle některých přesvědčivě demonstrována. Kritici metodě vyčítají, že jde o dost formální matematický přístup, který trpí následujícími nevýhodami:
- Předpokládá se, že složky jsou kulové, nanejvýš korigované koule (Kopal 1989,1990).
- Je nejisté, zda několik Fourierových koeficientů může obsahovat všechny informace ze světelné křivky. Metoda Fourierovské analýzy používá integrální moment pozorování, což dané pozorování vyhlazuje a tím maskuje příspěvek každého bodu k hodnotě A2m. Jednoduše se tím zahodí informace.
- Je nezbytné specifikovat škály svítivostí.
- Hodnota úhlu θ' pro první kontakt musí být stanovena přesně.
- Není snadné zavést do tohoto modelu další fyzikální efekty.
Budding (1993, str. 211) poznamenává, že ačkoli je metoda přímočará, v praktických situacích nastávají komplikace zejména proto, že vyjádření slapových deformací musí být velmi přesné a k tomu nejsou numericky získané veličiny Cj nejvhodnější. Celá procedura také ztrácí na jednoduchosti, pokud je zatmění jen částečné.
Poznámky: 1) Kopal používal pro označení ostatních metod založených na analýzách časových řad měření termín "time-domain" method.
Literatura:
Kopal, Z., 1941, ApJ 94, 145
Kopal, Z., 1946, Harvard observatory monograph, No. 6, Cambridge, Mass., Harvard univ. press
Kopal, Z., 1950, Harvard observatory monograph, No. 8, Cambridge, Mass., Harvard univ. press
Kopal, Z., 1955, Annales d'Astrophysique, 18, 379
Kopal, Z., 1959, Close Binary System, Internat. Astroph. Series, London, Chapman & Hall
Kopal, Z., 1975, A&AS 34, 431
Kopal, Z., 1979, Language of the Stars, D. Reidel, Dordrecht, Nizozemí
Kopal, Z., 1989, The Roche Problem, Kluwer Academic Publishers, Dordrecht, Nizozemí
Kopal, Z., 1990, Mathematical Theory of Stellar Eclipses, Kluwer Academic Publishers, Dordrecht, Nizozemí
Kopal, Z., Shapley, M. B., 1956, Jodrell Bank Ann. 1, 185
zpět na přehled metod