Čerepaščuk je zástupcem tzv. "ruské školy" modelování dvojhvězd, která je zaměřena na zákrytové dvojhvězdy s rozsáhlými atmosférami (Čerepaščuk 1966) jako například Wolfova-Rayetova dvojhvězda V444 Cyg (Čerepaščuk 1975, Čerepaščuk a Chaliulin 1976) a rentgenovské dvojhvězdy.
Modelové světelné křivky jsou většinou počítány za předpokladu sférických složek s rozšířenými prvky pro atmosférické zákryty, včetně disků. Problém nejmenších čtverců je řešen s velkou pozorností na existenci a jednoznačnost řešení (Čerepaščuk a kol. 1967). Metody jsou založeny na algoritmech uspořádání (Tichonov 1963a,b). Jejich popis lze najít také v knize Ceseviče (Čerepaščuk 1971, str. 278-282). Řešené modely popisují polopropustné zářivé disky obklopené nezářivou atmosférou. V nejjednodušším případě je disk hvězdy stejnorodý bez okrajového ztemnění. Neuvažuje se ani efekt odrazu. V případě rozsáhlých atmosfér je zřejmý rozdíl mezi poloměrem svítících disků a větších absorbujících disků. V Čerepaščukově zápisu jsou primární a sekundární složka rozlišeny podle vzdáleností ξ a ρ od středů disků. Svítivost soustavy pak lze zapsat ve tvaru
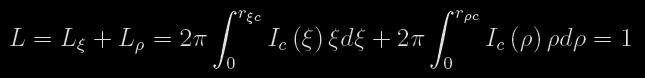(1)
kde rc vyjadřuje poloměr svítícího disku a Iρ a Iξ jsou toky záření z jednotky povrchu příslušné složky. Svítivost celé soustavy je normována k jedné. Během zákrytu hvězdy ρ je tok záření Ic(ρ) vycházející z jednotky povrchu dσ do prostorového úhlu dω absorbován atmosférou hvězdy ξ v rozsahu
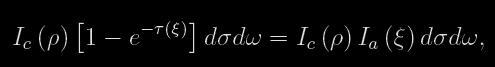(2)
kde
a a(r) je
absorpční koeficient v jednotce objemu hvězdy ξ a ρ je vzdálenost od středu této hvězdy. Pohlcené
záření musí být znovu vyzářeno v atmosféře hvězdy ξ a toto opětovné vyzáření by mělo být ekvivalentní
efektu odrazu (Goncharskii a kol. 1978). Ztráta světla během zákrytu je určena integrací přes zakrytou plochu
SΔ
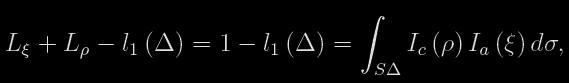(3)
kde l1 (Δ) je světlo viděné právě když je vzdálenost středů disků rovna Δ. Analogicky lze zapsat i pro světlo absorbované v atmosféře hvězdy ρ během sekundárního minima
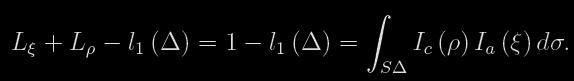(4)
Pro řešení je však nutné vyjádřit i vztah mezi Ic a Ia pomocí dvou apriorních relací ke vztahům (3) a (4). K tomu je zapotřebí znalost detailní struktury složek. Čerepaščuk navrhuje řešit problém použitím dvou modelů -- klasického a poloklasického. Klasický model v podstatě odpovídá "standardnímu" modelu se sférickými hvězdami, neprůhlednými disky a tenkými atmosférami s libovolným okrajovým ztemněním popsaným funkcemi Ic(ξ) a Ic(ρ), které vyplynou z řešení vztahů (3) a (4). Zmiňované apriorní funkce pro jednotlivé složky v tomto modelu jsou
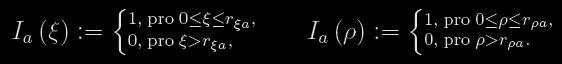(5)
Poloklasický model zahrnuje dle Čerepaščuka hvězdu jako v klasickém modelu a ještě "pekuliární hvězdu" s rozsáhlou atmosférou. Funkce Ic(ρ) a Ia(ρ) popisující tu "normální" hvězdu jsou známy. Naproti tomu emisní a absorpční vlastnosti pekuliární složky nejsou a priori známy a jsou určeny řešením vztahů (3) a (4). Tyto rovnice pak určují jen dvě funkce závisející na parametrech světelné křivky - poloměrech složek a sklonu trajektorie. K určení dalších parametrů je nutné vyřešit i vztah (1). Množství doplňkových vztahů pro kompletní řešení parametrů systému závisí na velikosti zakrývané části disků nebo jinak řečeno na tom, zda dochází k částečným nebo úplným zatměním. Čerepaščuk rozlišuje a dále diskutuje dva případy podle toho, zda cos i je větší nebo menší než poloměr normální složky. Konečně na základě důkladné analýzy pro klasické a poloklasické modely (Čerepaščuk 1971) usuzuje, že jednoznačné řešení je možné jen v těchto případech:
1. Klasické modely
(a) úplné zákryty,
(b) částečné zákryty pokud pro každé minimum je cos i menší než poloměr zakrývající hvězdy.
2. Poloklasické modely
(a) úplný zákryt pekuliární hvězdy normální složkou,
(b) částečné zákryty pokud je cos i menší než poloměr normální složky.
3. Poloklasické modely s neprůhledným jádrem
(a) úplné zákryty pekuliární hvězdy normální složkou,
(b) úplné zákryty normální hvězdy jádrem pekuliární hvězdy,
(c) částečné zákryty, je-li cos i menší než poloměr normální hvězdy.
K určení vymezených podmínek mohou být použity externí zdroje informací, například spektrofotometrie. Výše uvedené úvahy představují stručný nástin myšlenek zmiňované "ruské školy" silně orientované na otázky řešitelnosti a jednoznačnosti řešení modelů světelných křivek zejména pro systémy s jednou hvězdou s rozsáhlou atmosférou.
Literatura:
Cherepashchuk, A. M., 1966, Soviet Astronomy 10, 411
Cherepashchuk, A. M., 1971, Zatmenija šarovych zvjezd, potěmněnije kotorych proischodit po proizvolnomu zakonu, v Cesevič, V. P.: Zatmennyje peremennyje zvjezdy, vyd. Nauka, Moskva, str. 261-312
Cherepashchuk, A. M., 1975, (Astronomicheskii Zhurnal 52, no. 1, 1975, str. 81-91.) Soviet Astronomy 19, str. 47-53
Cherepashchuk, A. M.; Goncharskii, A. V.; Yagola, A. G., 1967, Soviet Astronomy 11, str. 990
Cherepashchuk, A. M.; Khaliullin, Kh. F., 1976, (Astronomicheskii Zhurnal 52, Nov.-Dec. 1975, str. 1214-1225.) Soviet Astronomy 19, no. 6, str. 727-734
Goncharskii, A. V.; Cherepashchuk, A. M.; Iagola, A. G., 1978, Numerical methods of solving inverse problems of astrophysics, Moscow, vyd. Nauka, 1978. 336 stran.
Tichonov, A. N., 1963a, Dokl. Akad. Nauk SSSR 153, 49-52
Tichonov, A. N., 1963b, Dokl. Akad. Nauk SSSR 151, 501-504
zpět na přehled metod