
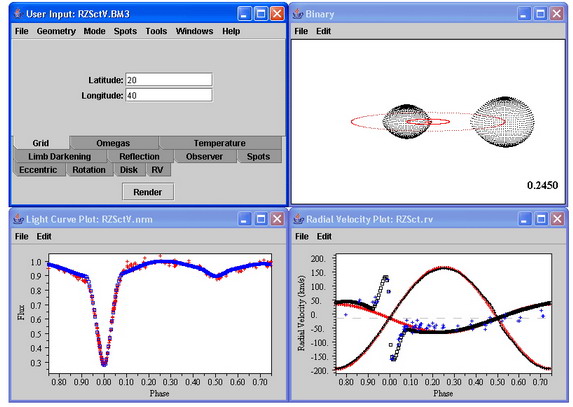
Jeho výhodou je velmi příjemné uživatelské prostředí se snadnými vstupy parametrů pro uživatele. Oproti ostatním programům má ale jisté zvláštnosti. Model je založen na Rocheovské geometrii, která je popisována pomocí sítě bodů, jejichž hustotu lze volit. Ekvipotenciální plochy vymezuje pomocí potenciálů Ω nebo C. Modifikovaný potenciál Ω slouží k popisu ekvipotenciální plochy vymezují povrch složek. Nabývá dvou mezních hodnot Ωin a Ωout. Pokud se povrch hvězdy nachází na vnitřní ekvipotenciální hladině Ωin, pak je složka přesně kontaktní. Vnější hladina Ωout znamená mez stability pro přesahující systémy. Potenciálu C používají i jiné modely, např. Mochnacki & Doughty (1972), Binnendijk (1977). Zde je definován takto C=2B1 Ω +B22 , kde B1 = 1/(1+q), B2 = q/(1+q), q = M2/M1. M1 a M2 jsou hmotnosti složek, zde chápané tak, že M1 je vždy hmotnější složka. Obvykle tedy q < 1, ale je-li méně hmotná složka teplejší, pak hlubší primární minima nastávají, když je tato hvězda zakryta. V takovém případě stejně jako pro W UMa systémy se poměr obrátí q > 1. Hmotnější hvězda zůstává označena indexem 1. Dalším parametrem popisujícím podobu soustavy je tzv. faktor vyplnění (fillout factor). Po stanovení poměru hmotností může být použit pro specifikaci kontaktních, přesahujících i oddělených dvojhvězd. Vyjadřuje míru, s jakou složky dvojhvězdy vyplňují své Rocheovské laloky. Je zde definováno takto
f = Ωin/Ω - 1 pro Ωin < Ω (složky nedosahující Rocheovy meze),
f= (Ωin-Ω)/(Ωin-Ωout)-1 pro Ωout≥ Ω (složky přesahující Rocheovu mez).
Pro oddělené soustavy je tedy -1 < f ≤ 0, zatímco pro přesahující 0≤ f≤1. Jinou definici faktoru vyplnění uvádějí Mochnacki & Doughty (1972)
F=(Ωin -Ω)/(Ωin -Ωout)+1 pro Ω < Ωin
F=Ωin/Ω pro Ω > Ωin.
Naproti tomu podobný přístup jako Bradstreet v BM3 použil Rucinski (1973)
fRucinski = (Ω -Ωout)/(Ωin -Ωout).
Počítaný model soustavy používá lineární okrajové ztemnění
I(θ)=I0(1-x-x.cosθ),
kde θ je úhel měřený mezi zorným paprskem a normálou k povrchu a I0 je intenzita měřená ve směru θ=0. Hodnoty okrajového ztemnění se dopočítávají z tabulek. Do roku 1993 byly se používaly tabulky Al-Naimiyho (1978), pak tabulky Van Hammeho (1993). Pro gravitační ztemnění a zjasnění se využívá výsledků práce von Zeipela (1924a,b) a Lucyho (1967). Efekt odrazu je charakterizován bolometrickým albedem. Pro hvězdy v zářivé rovnováze se předpokládá hodnota 1.00. Rucinski (1969) ukázal, že pro hvězdy s konvektivní obálkou (zde pro hvězdy chladnější než 7200 K) je toto albedo přibližně 0.50. Svítivost soustavy je normovaná k jedné jako v jiných modelech, svítivosti složek L1 , L2 jsou tedy relativní. Pokud je však zjištěno třetí světlo, je vyjádřeno ve stejných jednotkách jako vstupní nebo výstupní tok záření a není relativní jako L1 nebo L2.
BM3 umožňuje výpočet modelu s řadou světlých či tmavých kruhových skvrn, které je dokonce možné zadat s umbrou a penumbrou. Verze 3 je také rozšířena o možnost řešení excentrické trajektorie a asynchronní rotace složek. Parametricky je rotace vyjádřena pomocí rotačního parametru - poměru úhlové rychlosti rotace k oběžné úhlové rychlosti složky. Rotace je v základním nastavení zadána jako synchronní případně psedosynchronní. Pseudosynchroní rotaci, při ní je rotační úhlová rychlost shodná s úhlovou rychlostí oběhu v periastru, je možné popsat pro trajektorii s excentricitou e (Hut, 1981) parametrem
F2 =(1+e)/(1-e)3.
Do verze 3 byla také přidána možnost modelovat soustavu s diskem se skvrnami. Model disku je však velmi jednoduchý a navíc s podmínkou, že nedochází k zákrytu hvězdy diskem.
BM3 umožňuje řešit souběžně fotometrická i spektroskopická data, má bohatou grafickou výbavu. Na podpůrných www stránkách http://caleb.eastern.edu je databáze více než 300 vyřešených soustav různých typů, což může pomoci zejména začínajícím badatelům.
Sám autor doporučuje použití ve vysokoškolské výuce. Nicméně program má i svá omezení:
- Neiteruje automaticky k nejlepšímu řešení.
- Použití módu "vstup poloměru" není vhodné pro přesahující soustavy, protože vzhledem k definici může způsobit falešné výsledky.
- Výpočty svítivosti jsou založeny na Planckově zákonu absolutně černého tělesa. Další update zřejmě bude obsahovat i model atmosféry.
- Asynchronní rotace nebo excentrická trajektorie je nutné řešit ve sférických souřadnicích (počáteční nastavení) a ne ve válcových souřadnicích. Vážný problém to ale nepředstavuje, protože válcové souřadnice se používají pro přesahující soustavy, které mívají kruhové trajektorie a synchronní rotaci.
Literatura:
Al-Naimiy, H. M. K., 1978, A&AS 53, 181
Binnendijk, L., 1977, Vistas in Astronomy 21, 359
Bradstreet, D. H., The Society for Astronomical Sciences 24th Annual Symposium on Telescope Science, held May 24-26, 2005. Published by Society for Astronomical Sciences, 2005., p.23, ADS
Hut, P., 1981, A&A 99, 126
Lucy, L. B., 1967, Zeitschrift für Astrophysik 65, 89
Mochnacki, S. W., Doughty, N. A., 1972a, MNRAS 156, 51
Rucinski, S.M., 1969, Acta. Astron. 19, 245
Rucinski, S. M., 1973, Acta Astronomica 23, 79
Van Hamme, W., 1993, AJ 106, 2096
von Zeipel, H., 1924a, MNRAS 84, 702
von Zeipel, H., 1924b, MNRAS 84, 665